Divide and Conquer & Time Compute

⭐文章目录⭐

• Divide and Conquer
  • Counting Inversions
  • Closest Pair of Points
• Time Compute
  • Recursion Tree Method
  • Master Theorem
  • Enhanced Master Theorem
  • Substitution Method

👇

Divide and Conquer

Divide a problem into smaller subproblems, solve each subproblem independently, and then combine the solutions to the subproblems to solve the original problem.

Counting Inversions

Given an array of n distinct integers, count the number of inversions in the array. An inversion is a pair of indices $(i, j)$ such that $i < j$ and $a[i] > a[j]$.

Solutions

Bruteforce solution: $O(n^2)$ time complexity.

D&C: O(nlogn) time complexity.

• Divide the array into two halves.
• Count the number of inversions in each half recursively.
• Count the number of inversions in the different halves.

Sort-and-CountInv(A):
    if n <= 1:
        return (A,0)
    else:
        L=left half of A
        R=right half of A
        (B,LInv)=Sort-and-CountInv(L)
        (C,RInv)=Sort-and-CountInv(R)
        (D,SInv)=Merge-and-Sort(B,C)
        return (D,LInv+RInv+SInv)

Merge-and-Sort(B,C):
    i=0, j=0, SInv=0
    for k in range(n):
        if B[i] <= C[j]:
            D[k]=B[i]
            i=i+1
        else:
            D[k]=C[j]
            j=j+1
            SInv=SInv+n/2-i+1
    return (D,SInv)

We have

$$\begin{cases}T(n)=2T(n/2)+O(n)\\T(1)=O(1)\end{cases}$$

Therefore, the time complexity is $O(nlogn)$.

Closest Pair of Points

Given n points in the plane, find the two points that are closest to each other.

Solutions

$\Delta_1=closest Left Pair$
$\Delta_2=closest Right Pair$
$\Delta=min(\Delta_1,\Delta_2)$

1.Watching this picture, when we want to find the closest pair in the split part, we first find a point $p$ ,whose distance to the cut line is less than $\Delta$.
2.Then we can cut the plane into eight parts of $\Delta/2\times\Delta/2$ square, and each part can have at most 1 point.
3.Then we only need to find the closest pair in the divided parts and go through all the points whose distance to the cut line is less than $\Delta$.

Px=sort P by X
Py=sort P by Y
closestPair(Px,Py):
    if n<=3:
        return bruteforce(Px)
    else:
        Lx= pts on the left half,sorted by X
        Ly= pts on the left half,sorted by Y
        Rx= pts on the right half,sorted by X
        Ry= pts on the right half,sorted by Y
        (L1,L2)=closestPair(Lx,Ly)
        (R1,R2)=closestPair(Rx,Ry)
        d=min(dist(L1,L2),dist(R1,R2))
        (s1,s2)= closestSplitPair(Px,Py,d)
        return the_closest_pair((L1,L2),(R1,R2),(s1,s2))

closestSplitPair(Px,Py,d):
    x'=largest x of Pts in left half
    S={q1,q2,...,qk}(x'-d <= q <= x'+d)(sorted by y)
    minDist = +inf
    for i=1 to k:
        for j= 1 to 8:
            if (dist(qi,qi+j) < minDist):
                minDist=dist(qi,qi+j)
                closestPair=(qi,qi+j)
    return closestPair

The time complexity is $O(nlogn)$.

Time Compute

$$\begin{cases}T(1)=1\\T(n)=aT(\frac{n}{b})+n^c\end{cases}$$

Solutions

Recursion Tree Method

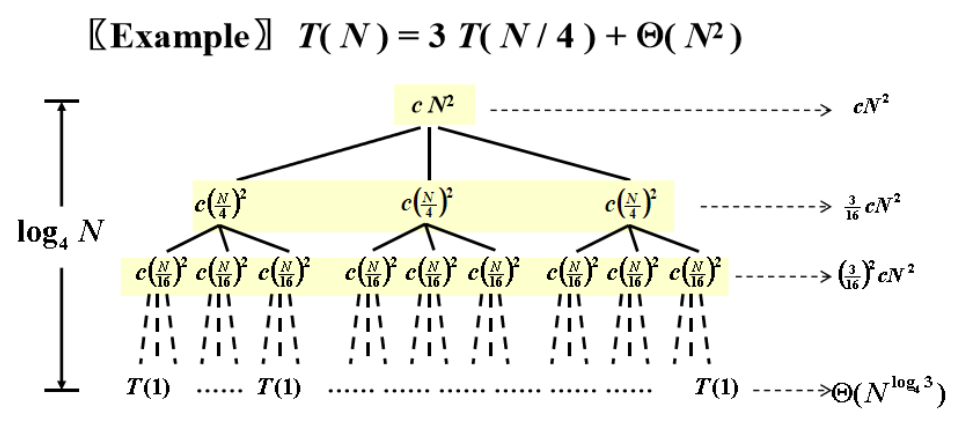
$$T(n)=\sum_{i=0}^{log_4(n)-1}(\frac{3}{16})^icN^2+\Theta(N^{log_4(3)})=O(N^2)$$

• If the running time of per level decreases, select the first level.
• If the running time of per level increases, select the last level.
• If the running time of per level is the same, total time=per level time $\times$ number of levels.

Master Theorem

$$\begin{cases}T(1)=1\\T(N)=aT(\frac{N}{b})+f(N)(or\ N^c)\end{cases}$$

• If $f(N)=O(N^{log_b{a-\varepsilon}})$, or $\frac{a}{b^c}>1$, $T(N)=\Theta(N^{log_b{a}})$.
• If $f(N)=\Theta(N^{log_b{a}})$, or $\frac{a}{b^c}=1$, $T(N)=\Theta(log_b{N}N^c)$.
• If $f(N)=\Omega(N^{log_b{a+\varepsilon}})$, or $\frac{a}{b^c}<1$, $T(N)=\Theta(f(N))$.

Enhanced Master Theorem

Substitution Method

Guess and proof.